Activité - Distance entre deux points

Mesurer : Déterminer, évaluer avec un instrument de mesure, le volume, la superficie, la quantité de quelque chose
Calculer : Déterminer par le calcul numérique, évaluer, compter une somme, une mesure, une distance, etc.

Exercice 1 Sur votre cahier, tracer un repère orthonormé \((O;I;J)\) avec \(OI=OJ=1cm\).

1 Dans le repère, placer les points \(A (-1;1)\) et \(B (3;4)\). Le but de l'exercice est de calculer la distance \(AB\).

2 Placer le point \(C (3;1)\). Quelles sont, en centimètres, les valeurs de \(AC\) et \(CB\) ? Justifier.

3 Tracer le triangle \(ABC\). En utilisant un théorème connu, calculer la valeur de \(AB\) en centimètres.

Exercice 2 Le but de cet exercice est de trouver une formule pour exprimer la distance entre deux points \(A (x_A;y_A)\) et \(B (x_B;y_B)\) quelconqu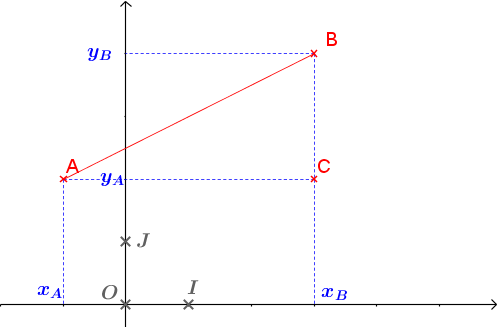es.

On place le point \(C\) de coordonnées \((x_B;y_A)\) de manière à former un triangle \(ABC\) rectangle avec \((AC)\) et \((CB)\) parallèles aux axes.

1 On cherche une formule pour exprimer la distance \(AC\) :

Exprimer \(AC\) à l'aide d'une formule utilisant \(x_A\) et \(x_C\) seulement.
Comparer \(x_C\) et \(x_B\).
En déduire une formule exprimant \(AC\) en fonction de \(x_A\) et \(x_B\).

2 On cherche une formule pour exprimer \(BC\) :

Exprimer \(BC\) à l'aide d'une formule utilisant \(y_B\) et \(y_C\) seulement.
Comparer \(y_C\) et \(y_A\).
En déduire une formule exprimant \(BC\) en fonction de \(y_A\) et \(y_B\).

3 On cherche une formule pour exprimer \(AB\) sans avoir besoin du point \(C\).

Le triangle \(ABC\) est rectangle en \(C\). En rappelant un théorème connu, exprimer la longueur \(AB\) en fonction des longueurs \(BC\) et \(AC\).
En déduire, en utilisant les question précédentes, une formule exprimant \(AB\) en fonction de \(x_A\), \(x_B\), \(y_A\) et \(y_B\).